“Learning by doing”, “Übung macht den Meister” oder “Aus Fehlern lernt man” – warum diese Phrasen nicht nur für uns Menschen motivierend sind, sondern auch mathematischen Algorithmen zum Erfolg verhelfen, erfahren Sie in diesem Beitrag. Für komplexe Problemstellungen in Wirtschaft und Industrie werden Optimierungsmodelle und Lösungsalgorithmen täglich verwendet, um schwierige Entscheidungen zu treffen. Dabei sind die meisten EntscheidungsträgerInnen mit einem hochdynamischen Umfeld, unsicheren Prognosen und unzähligen Variablen konfrontiert. Um mit diesen Herausforderungen umgehen zu können und enormen Rechenaufwand einzusparen, werden Methoden entwickelt, die mit Hilfe von künstlicher Intelligenz funktionieren. Klassische Optimierungsverfahren werden mit maschinellem Lernen kombiniert, um den hohen Anforderungen gerecht zu werden – denn eines kann gesagt werden: Optimierung will gelernt sein.
Inhalt
Erfolgreich sein, heißt gute Entscheidungen zu treffen. Doch wann ist eine Entscheidung optimal und vor allem, wie findet man diese? Wie viel Paar Skier soll ein Sportartikelhersteller produzieren, wenn deren Nachfrage nur geschätzt werden kann? Wie viele Aktienanteile soll eine Investorin für ihr Portfolio ankaufen, wenn der zukünftige Aktienkurs höchst unsicher ist? Oder an welchen Orten sollen COVID-19 Testzentren errichtet werden, um möglichst vielen Menschen eine unkomplizierte Anfahrt zu gewährleisten? So unterschiedlich diese Anwendungen auch klingen mögen – sie alle haben eines gemeinsam – optimale Entscheidungen werden gesucht. Bewährte Werkzeuge zur Entscheidungsunterstützung sind mathematische Optimierungsmodelle, die reale Probleme auf ihre wesentlichen Merkmale herunterbrechen. Für diese Modelle können dann, durch den Einsatz von Lösungsverfahren, bestmögliche Entscheidungen gefunden und auf die realen Problemstellungen angewandt werden. Die Ansprüche der Wirtschaft und Industrie an diese mathematischen Modelle werden allerdings immer höher, die Problemstellungen immer komplexer und Aspekte wie schwankende Parameter und dynamische Umgebungen immer relevanter. Diese Entwicklung führt dazu, dass klassische exakte Lösungsverfahren Stunden, Tage oder sogar Wochen benötigen würden, um Entscheidungen unter realistischen Bedingungen zu berechnen. Gleichzeitig steigt die Verfügbarkeit einer großen Menge an Daten, vor allem angetrieben durch den technologischen Fortschritt und die voranschreitende Digitalisierung industrieller Prozesse. So beschäftigt sich ein neuer Trend mit der Verschmelzung von Methoden der klassischen Optimierung mit Ansätzen des maschinellen Lernens zu effizienten datengetriebenen Lösungsverfahren. Diese Verfahren sollen in der Lage sein, durch Techniken der künstlichen Intelligenz, Muster in den Problemeigenschaften zu finden, komplexe Zusammenhänge zu vereinfachen und vielversprechendes Lösungsverhalten zu erlernen. Das Ziel ist es dabei, das Beste aus den Welten der Optimierung und des maschinellen Lernens zu kombinieren, um selbst für hochkomplexe Entscheidungsprobleme gute Lösungen in angemessener Zeit zu finden.
Zur Entscheidungsfindung wird ein mathematisches Modell als Abbild der Realität erstellt, bei dem es eine Zielfunktion unter Einhaltung verschiedener Restriktionen zu optimieren gilt. Um eine optimale Lösung für ein Model zu finden, gibt es zwei verschiedene Ansätze. Einerseits können exakte Lösungsverfahren angewandt werden, die bei Auffinden einer Lösung auch deren globale Optimalität garantieren können. Diese Lösungsverfahren benötigen aber in der Regel enormen Rechenaufwand und liefern besonders für große und realistische Modelle oft keine Lösung in angemessener Zeit. Neben den exakten Verfahren existiert auch die Gruppe der heuristischen Lösungsverfahren. Dabei handelt es sich um Algorithmen, die auf konkrete Problemstellungen zugeschnitten wurden, um in kurzer Zeit gute Lösungen zu finden. Es kann dabei allerdings keine Aussage getroffen werden, ob es sich bei der Lösung um ein globales Optimum handelt. Den heuristischen Verfahren übergeordnet sind die sogenannten Metaheuristiken. Diese beschreiben eine allgemeine algorithmische Vorgangsweise, die auf eine Vielzahl an Problemstellungen anwendbar ist.
Ansätze des maschinellen Lernens können nun mit beiden Arten von Lösungsverfahren kombiniert werden. Bei exakten Methoden soll dies meist eine Verringerung des Rechenaufwandes bewirken, indem die künstliche Intelligenz vielversprechende Bereiche des Lösungsraums auffindet, effiziente Ausführungsreihenfolgen innerhalb des Algorithmus bestimmt oder die Zielfunktionswerte schneller berechnet. Bei heuristischen Methoden geht es vorwiegend darum, durch den Einsatz von lernenden Algorithmen bessere Lösungsqualitäten zu erzeugen. Dabei sollen vor allem Aufgaben wie Parameter Tuning, Algorithmus-Auswahl oder Operator-Management durch die Machine Learning Methode übernommen werden.
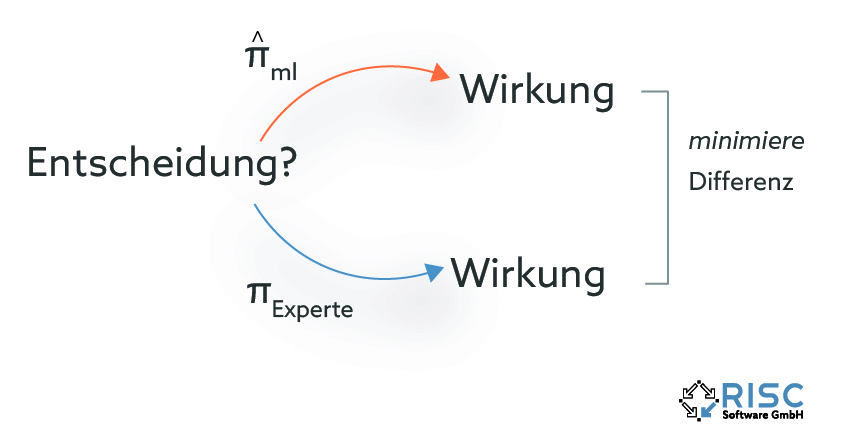
Spricht man von Verfahren der Optimierung, die einen lernenden Aspekt beinhalten, so lassen sich grundsätzlich zwei Arten von Lernmethoden unterscheiden. Diese beiden Arten haben ihren Ursprung in zwei verschiedenen Motivationen zur Anwendung solcher Algorithmen. In manchen Bereichen besteht bereits umfassendes theoretisches oder empirisches Wissen eines Experten über das Entscheidungsumfeld, das durch eine exakte Optimierungsmethode abgebildet werden könnte. Der Anwender möchte nun den lernenden Algorithmus dazu verwenden, dieses bekannte Wissen zu approximieren und somit erheblichen Rechenaufwand einzusparen. Es soll eine Verhaltensregel oder auch “policy” (πml) erlernt werden, die die Entscheidungen des Experten (πExperte) imitiert und somit ähnliche Resultate erzielt. Bei dieser Art des Lernens versucht der Algorithmus nicht, die Qualität der Resultate zu optimieren, sondern minimiert die Diskrepanz zwischen den getroffenen Entscheidungen und den Demonstrationen des Experten.
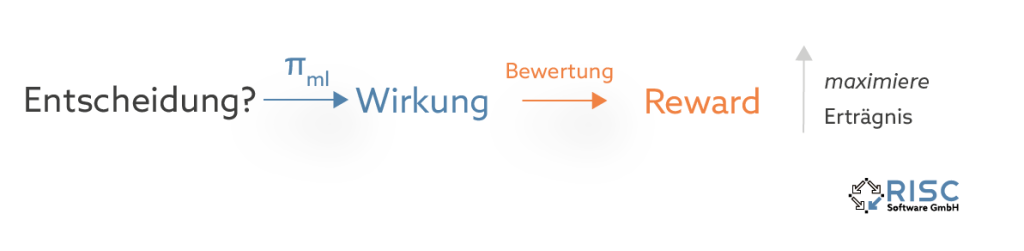
Es kommt allerdings auch vor, dass nicht genügend Informationen über das Entscheidungsumfeld vorhanden sind und neue Entscheidungsstrategien entwickelt werden sollen. Für diesen Fall wird der lernende Algorithmus in einem trial and error setting darauf trainiert, ein sogenanntes reward signal zu maximieren. Bei dieser Art des Lernens erforscht der Algorithmus selbständig den Entscheidungsraum und gewinnt mit jedem Erkundungsschritt neue Informationen über die Qualität von getroffenen Entscheidungen.
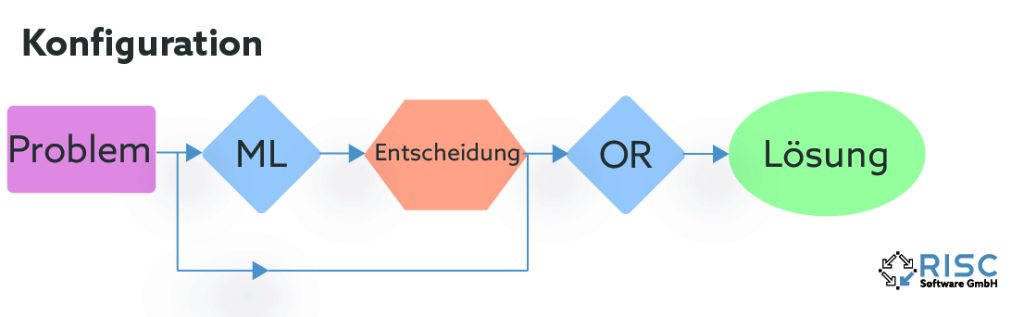
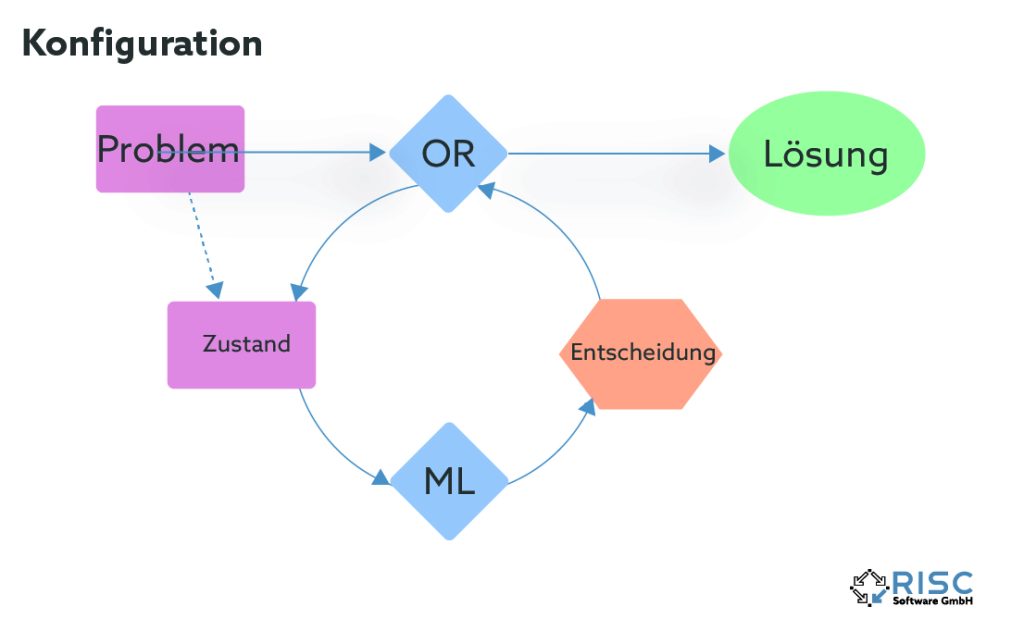
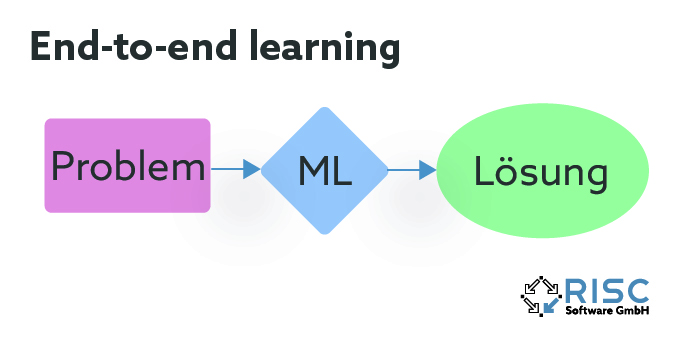
Die vorgestellten Methoden lassen sich nicht nur hinsichtlich ihrer Art des Lernens gliedern, sondern auch in welcher Struktur der Lernprozess in den Algorithmus eingebunden wird. Maschinelles Lernen kann im Vorhinein verwendet werden, um die Optimierungsmethode zu konfigurieren, beispielsweise durch Erlernen vielversprechender Parameter oder Ausführungsreihenfolgen innerhalb des Algorithmus. Eine andere Möglichkeit besteht darin, maschinelles Lernen und Optimierungsmethode abwechselnd iterativ auszuführen. Dabei gibt der Optimierungsalgorithmus laufend Informationen zur aktuellen Lösungsqualität an den lernenden Teil ab, während dieser wiederum neue vielversprechende Lösungsbereiche aus den Informationen ableitet und zurückgibt. Bei der dritten Variante ersetzt der lernende Teil das eigentliche Optimierungsverfahren und ermittelt zu einem gegebenen Problem bereits eine fertige Lösung. In diesem Fall spricht man auch von “end-to-end learning”.
Nachdem die Frage “wie” gelernt wird geklärt ist, bleibt noch die viel wichtigere Frage offen – was wird nun eigentlich genau erlernt? Dafür gibt es verschiedene Ansätze, abhängig von den jeweiligen Eigenschaften der verwendeten Optimierungsmethode und problemspezifischen Faktoren.
Metaheuristiken enthalten in der Regel etliche Parameter, die signifikanten Einfluss auf die Performance haben. Maschinelles Lernen kann eingesetzt werden, um diese Parameter für eine bestimmte Problemklasse oder auch für einzelne Instanzen eines Problems zu erlernen. Dabei kommen vor allem Techniken der linearen oder logistischen Regression, neuronale Netze oder response surface Methoden zum Einsatz.
Für komplexe Probleme ist die Auswertung der Zielfunktion mit hohem Rechenaufwand verbunden. Maschinelles Lernen kann verwendet werden, um eine Approximation der Zielfunktion zu erstellen und somit die Auswertung zu beschleunigen. Polynomielle Regression, neuronale Netzwerke oder Markov fitness models sind populäre ML Methoden, die dafür infrage kommen.
Viele Metaheuristiken (etwa lokale Suchverfahren) verwenden Operatoren, um ausgehend von bereits erzeugten Lösungen neue vielversprechende Lösungen zu generieren. Bei genetischen Algorithmen spricht man auch von Populationen, die durch Mutations- und Kreuzungsoperatoren verändert werden. Oft wird der Einsatz dieser Operatoren schon im Vorhinein durch fixe Regeln basierend auf den Lösungseigenschaften vorgeschrieben. Diese Regeln können allerdings auch durch maschinelles Lernen ständig angepasst und verbessert werden. So eignen sich beispielsweise inverse neuronale Netze oder Klassifikationsalgorithmen aus dem Bereich der symobolic learning Methoden, um Regeln zu erlernen, die bereits erfolgte Fehlversuche nicht wiederholen und erklären können, warum manche Operatoren an dieser Stelle besser geeignet sind als andere.
Es kann vorkommen, dass ein ganzes Portfolio an verschiedenen Lösungsmethoden für dieselbe Problemklasse zur Verfügung steht und man daran interessiert ist, welche davon die beste Performance liefert. Das algorithm selection problem beschreibt genau diesen Sachverhalt, bei dem eine Lösungsmethode a aus der Menge der verfügbaren Methoden A so gewählt werden soll, dass die Performance von a, angewandt auf ein Problem x, unter allen Methoden in A bestmöglich ist. Dieses Auswahlproblem soll unter Abhängigkeit der Problemeigenschaften des Problems x gelöst werden. Klassifizierungsalgorithmen und neuronale Netze eignen sich, um das verfügbare Portfolio A basierend auf den Problemeigenschaften in mehr oder weniger vielversprechende Methoden zu unterteilen.
Das Branch and Bound Framework ist ein weit verbreitetes exaktes Lösungsverfahren. Dabei wird die Problemstellung Stück für Stück in kleinere Teilprobleme zerlegt (“Branching”) und lässt sich in einer Baumstruktur (“Branch and Bound Tree” / “Suchbaum”) darstellen, in der jeder Knoten eine unvollständige Lösung des Gesamtproblems repräsentiert. Für diese Knoten können dann durch Lockerung der Restriktionen untere Schranken berechnet werden. Gleichzeitig können durch heuristisches Lösen der Teilprobleme obere Schranken gefunden werden und sobald für einen Knoten im Suchbaum die untere Schranke über der oberen Schranke liegt, kann der gesamte “Ast” verworfen werden, was wiederum den Suchraum einschränkt. (“Bounding”). Je schneller gute obere Schranken gefunden werden, desto schneller können ganze Bereiche des Suchraums verworfen werden, was zu einer erheblichen Performancesteigerung des Branch and Bound Algorithmus führt. Um solche oberen Schranken zu erhalten werden verschiedene Heuristiken eingesetzt, die in jedem Knoten versuchen eine zulässige gute Lösung zu generieren. Es ist allerdings stark vom jeweiligen Problem und von der jeweiligen Instanz abhängig, welche vorhandene Heuristik die besten Ergebnisse liefert. Es wünschenswert, die jeweils beste Heuristik früh einzusetzen und nicht davor, mit schlechteren Heuristiken Zeit zu verschwenden. Üblicherweise wird die Ausführungsreihenfolge der Heuristiken im Vorhinein definiert, unabhängig von der jeweiligen Probleminstanz und unfähig auf dynamische Änderungen während des Suchlaufs zu reagieren. Ein neuer Ansatz verbessert die Ausführungsreihenfolge der Heuristiken datenbasiert und passt sie während des Suchlaufs ständig an.
In einer Zeit, in der große Mengen an Daten bei nahezu jedem Prozess gesammelt werden, ist es naheliegend, diese in der Entscheidungsfindung zu berücksichtigen und die dazu verwendeten Optimierungsalgorithmen mit lernenden Komponenten zu unterstützen. Der Einsatz von maschinellem Lernen hat das Potenzial, den Rechenaufwand exakter Lösungsverfahren zu verringern und die Lösungsqualität heuristischer Verfahren zu verbessern. Die Verschmelzung der beiden Welten “klassische Optimierung” und “künstliche Intelligenz” liegt im Trend und man darf gespannt sein, welche Resultate die Forschung auf diesem interdisziplinären Gebiet noch erzielen kann. Eines steht jedenfalls fest, es ist spannend, wie vielfältig die beiden Ansätze kombiniert werden können und wie sich Ergebnisse dadurch verbessern lassen – gelernt ist eben einfach gelernt!
Mathematical Optimization Engineer
