“Learning by doing“, “Practice makes perfect“ or “You learn from mistakes“ – why these phrases are not only motivating for us humans, but also help mathematical algorithms to succeed, you will learn in this article. For complex problems in business and industry, optimization models and solution algorithms are used every day to make difficult decisions. In doing so, most decision makers are confronted with a highly dynamic environment, uncertain forecasts and countless variables. In order to deal with these challenges and to save enormous computational effort, methods are being developed that work with artificial intelligence. Classical optimization methods are combined with machine learning to meet the high demands – because one thing can be said: Optimization has to be learned.
Table of contents
Being successful means making good decisions. But when is a decision optimal and, above all, how do you find it? How many pairs of skis should a sporting goods manufacturer produce when their demand can only be estimated? How many shares of stock should an investor buy for her portfolio when the future stock price is highly uncertain? At which locations should COVID-19 test centers be set up to provide easy access to as many people as possible? As different as these applications may sound, they all have one thing in common: Optimal decisions are sought. Proven decision support tools are mathematical optimization models that break down real-world problems to their essential features. For these models, best possible decisions can then be found and applied to the real problems by using solution methods.
However, the demands of business and industry on these mathematical models are becoming ever higher, the problems increasingly complex, and aspects such as fluctuating parameters and dynamic environments ever more relevant. This development leads to the fact that classical exact solution methods would need hours, days or even weeks to calculate decisions under realistic conditions. At the same time, the availability of a large amount of data is increasing, mainly driven by technological progress and the advancing digitalization of industrial processes. Thus, a new trend deals with the fusion of methods of classical optimization with machine learning approaches to efficient data-driven solution methods. These methods are able to use artificial intelligence techniques to find patterns in problem properties, simplify complex relationships and learn promising solution behavior. The goal here is to combine the best of the worlds of optimization and machine learning to find good solutions in a reasonable amount of time, even for highly complex decision problems.
For decision-making, a mathematical model is created as a representation of reality, in which an objective function has to be optimized while complying with various restrictions. There are two different approaches to find an optimal solution for a model. On the one hand, exact solution methods can be applied, which can also guarantee their global optimality if a solution is found. However, these solution methods usually require enormous computational effort and often do not provide a solution in a reasonable time, especially for large and realistic models. Besides the exact methods, there is also a group of heuristic solution methods. These are algorithms that have been tailored to concrete problems in order to find good solutions in a short time. However, no statement can be made whether the solution is a global optimum. The so-called metaheuristics are superordinate to the heuristic methods. These describe a general algorithmic procedure, which is applicable to a multiplicity of problem definitions.
Machine learning approaches can now be combined with both types of solution methods. For exact methods, this is mostly to reduce computational effort by having the artificial intelligence find promising regions of the solution space, determine efficient execution orders within the algorithm, or compute the objective function values faster. Heuristic methods are predominantly concerned with generating better solution qualities through the use of learning algorithms. In particular, tasks such as parameter tuning, algorithm selection or operator management are to be taken over by artificial intelligence.
If one speaks of methods of optimization which contain a learning aspect, then basically two types of learning methods can be distinguished. These two types have their origin in two different motivations for applying such algorithms. In some areas, experts already have extensive theoretical or empirical knowledge about the decision environment, which could be represented by an exact optimization method. The users now want to use the learning algorithm to approximate this known knowledge and thus save considerable computational effort. The goal is to learn a behavioral rule or “policy“ (πml) that imitates the decisions of the experts (πexpert) and thus achieves similar results. In this type of learning, the algorithm does not try to optimize the quality of the results, but minimizes the discrepancy between the decisions made and the expert*s demonstrations.
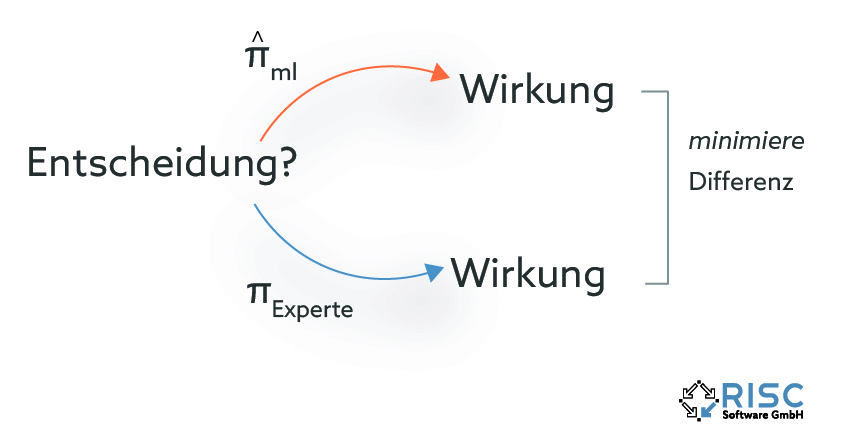
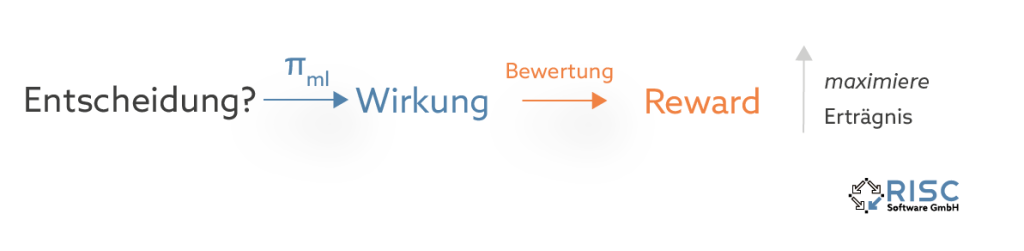
However, it also happens that there is not enough information about the decision environment and new decision strategies should be developed. In this case, the learning algorithm is trained in a trial-and-error setting to maximize a so-called reward signal. In this type of learning, the algorithm independently explores the decision space and gains new information about the quality of decisions made with each exploration step.
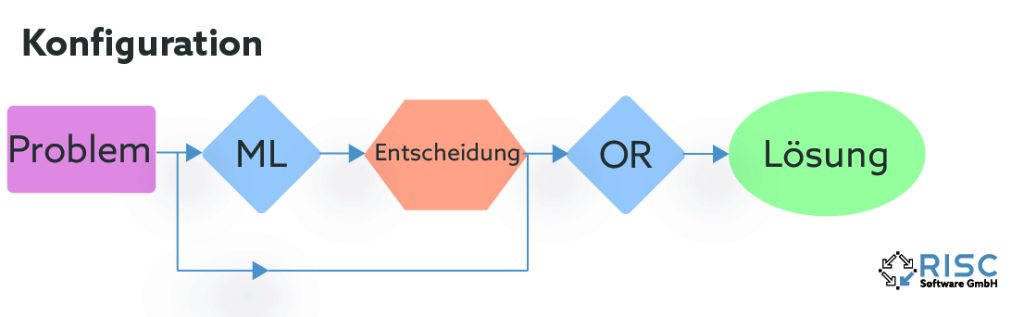
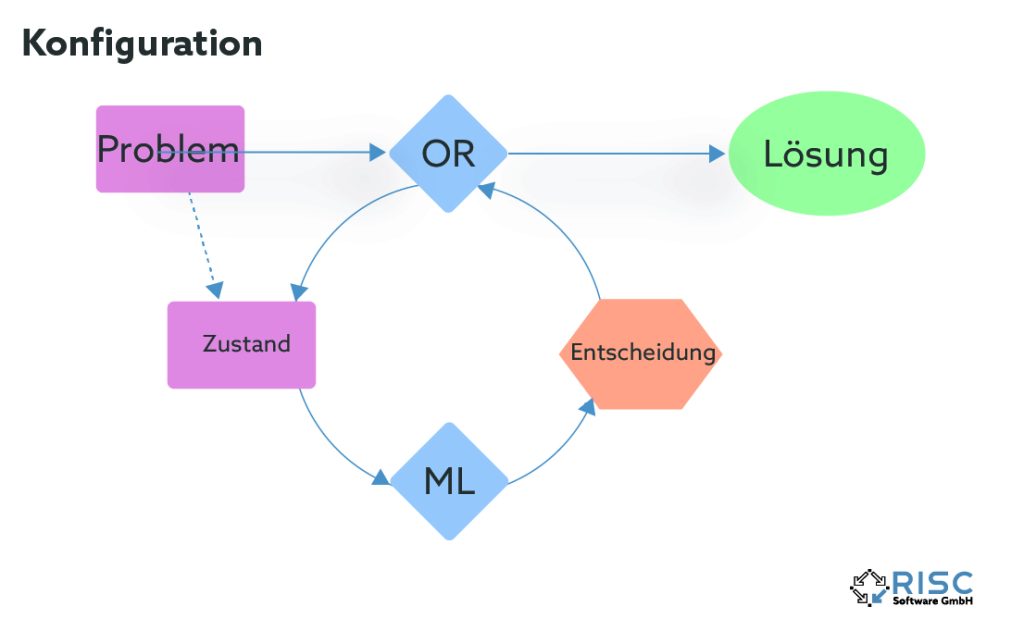
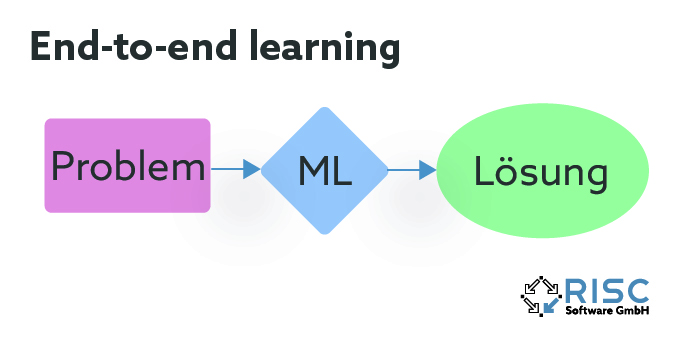
The methods presented can be divided not only in terms of how they learn, but also in terms of the structure in which the learning process is incorporated into the algorithm. Machine learning can be used in advance to configure the optimization method, for example by learning promising parameters or execution sequences within the algorithm. Another option is to alternate machine learning and the optimization method by iterative iteratively. In this case, the optimization algorithm continuously feeds information about the current solution quality to the learning part, while the learning part in turn derives and feeds back new promising solution domains from the information. In the third variant, the learning part replaces the actual optimization procedure and already determines a finished solution to a given problem. In this case, we also speak of end-to-end learning.
After the question of how learning takes place has been clarified, the much more important question remains unanswered: What exactly is learned? There are different approaches to this question, depending on the properties of the properties of the optimization method used and problem-specific factors.
Metaheuristics usually contain a number of parameters that have a significant impact on performance. Machine learning can be used to learn these parameters for a specific class of problem or for individual instances of a problem. Techniques of linear or logistic regression, neural networks or response surface methods are particularly used.
For complex problems, evaluating the objective function requires a lot of computational effort. Machine learning can be used to create an approximation of the objective function and thus speed up the evaluation. Polynomial regression, neural networks or Markov fitness models are popular ML methods that can be used for this purpose.
Many metaheuristics (such as local search methods) use operators to generate new promising solutions starting from already generated solutions. In genetic algorithms, we also talk about populations that are modified by mutation and crossover operators. Often, the use of these operators is prescribed in advance by fixed rules based on the solution properties. However, these rules can also be continuously adapted and improved by machine learning. For example, inverse neural networks or classification algorithms from the field of symobolic learning methods are suitable for learning rules that do not repeat previous failed attempts and can explain why some operators are more suitable than others at this point.
It may happen that a whole portfolio of different solution methods is available for the same problem class and one is interested in which of them provides the best performance. The algorithm selection problem describes exactly this situation, in which a solution method a is to be selected from the set of available methods A in such a way that the performance of a, applied to a problem x, is best possible among all methods in A. This selection problem is to be solved depending on the problem properties of the problem x. This selection problem is to be solved depending on the problem properties of problem x. Classification algorithms and neural networks are suitable to divide the available portfolio A into more or less promising methods based on the problem properties.
The branch-and-bound framework is a widely used exact solution method. The problem is broken down piece by piece into smaller subproblems (“branching“) and can be represented in a tree structure (“branch and bound tree“ / “search tree“), in which each node represents an incomplete solution of the overall problem. Lower bounds can then be computed for these nodes by relaxing the restrictions. At the same time, upper bounds can be found by heuristically solving the subproblems, and as soon as the lower bound is above the upper bound for a node in the search tree, the entire “branch“ can be discarded, which in turn restricts the search space (“bounding“). The faster good upper bounds are found, the faster entire regions of the search space can be discarded, resulting in a significant performance improvement of the branch-and-bound algorithm. To obtain such upper bounds, various heuristics are used that attempt to generate an admissible good solution in each node. However, it is highly dependent on the particular problem and instance which existing heuristic yields the best results. It would be desirable to use the best heuristic in each case early and not waste time with worse heuristics beforehand. Typically, the execution order of heuristics is defined in advance, independent of the particular problem instance and incapable of responding to dynamic changes during the search run. A new approach improves the execution order of heuristics in a data-based manner and continuously adjusts it during the search run.
In an era where large amounts of data are collected in almost every process, it is obvious to take them into account in decision making and to support the optimization algorithms used for this purpose with learning components. The use of machine learning has the potential to reduce the computational cost of exact solution methods and improve the solution quality of heuristic methods. The fusion of the two worlds of “classical optimization“ and “artificial intelligence“ is in vogue, and one can be curious to see what results research in this interdisciplinary field can still achieve. In any case, one thing is certain: It is exciting to see how diverse the two approaches can be combined and how results can be improved as a result – learned is simply learned!
Mathematical Optimization Engineer
